Создание модели инерции в ходе теннисного матча

Создание модели инерции в ходе теннисного матча

В этой статье Джонатон Брицки рассказывает о разработке уточненной версии созданной им модели анализа воздействия инерции в теннисе на участников различных рынков ставок.

Обзор сильных и слабых сторон модели

В первой части этой статьи я объяснил подход к созданию модели инерции, которая имеет место в перерывах между сетами теннисного матча. В рамках этого подхода используются доли очков, которые могут быть выиграны на подаче. При этом я показал, что корректировка ожиданий по поводу долей очков, которые могут быть выиграны на подаче, лишь в конце каждого сета обеспечивает недостаточную динамичность. По этой причине представленная модель обладает определенными ограничениями: с ее помощью нельзя оценивать ставки на тотал и ставки с гандикапом.

Во второй части статьи я опишу новые элементы модели, которые лучше отражают инерцию как в течение сетов, так и в перерывах между сетами теннисного матча.

В первой части статьи я продемонстрировал, что вероятность победы игрока во втором сете в среднем повышается, если он победил в первом сете. Первым шагом к построению более динамичной модели является определение отношения перевеса в счете первого сета к победителю во втором сете и перевесу в счете второго сета.

Измерение инерции в первом и втором сетах

На приведенном ниже графике показано, как перевесы в счете первого сета матча относятся к долям побед тех же игроков во втором сете. Например, игроки, предполагаемая вероятность победы которых в матче составляет 71–80 % и которые победили в первом сете с перевесом в пять или шесть геймов (то есть со счетом 6:1 или 6:0), выигрывают второй сет в 83 случаях из 100.

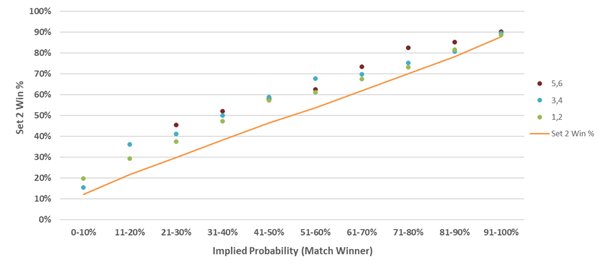
По всей видимости, между перевесом в счете первого сета и исходом второго сета существует однозначная прямая зависимость. Эта зависимость разрушается в связи со слабейшими аутсайдерами, предполагаемая вероятность победы которых в матче составляет менее 20 %, хотя количество матчей в этом диапазоне сравнительно невелико. Можно немного углубиться в изучение полученного результата и сравнить перевес в счете первого сета с перевесом счета второго сета.

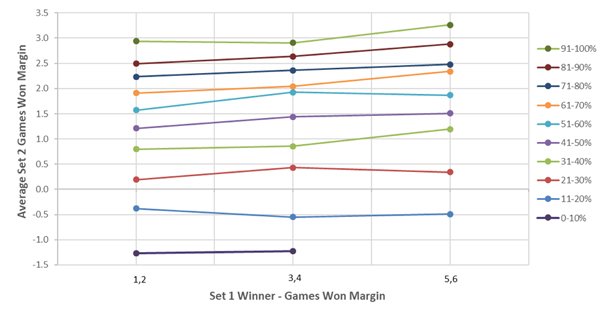
Здесь вновь наблюдается эффект инерции. Больший перевес в счете первого сета в среднем влечет за собой больший перевес в счете второго сета. Получив эти результаты, я скорректировал среднее изменение доли очков, которые могут быть выиграны на подаче, для второго сета. При этом мои действия совпадали с описанными в первой части этой статьи.

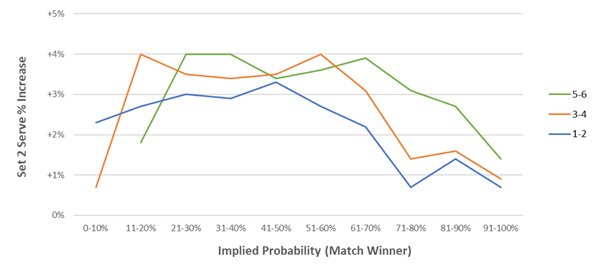
Теперь нам известен коэффициент корректировки доли очков, которые могут быть выиграны на подаче во втором сете; эту корректировку следует выполнить по окончании первого сета (с учетом перевеса в счете этого сета). Как бы то ни было, мы хотим выполнять корректировку чаще – после каждого гейма или в идеале после получения каждого очка. В качестве следующего шага мы определим нарастающие корректировки, которые нужно выполнять в ходе сета.

Чтобы выяснить зависимость между долями очков, выигранных на подаче, и счетами сетов (а вместе с ней и коэффициент необходимой корректировки), я смоделировал 30 000 матчей и вычислил разницу в долях очков, выигранных на подаче, связанную с различными счетами сетов.

Для отражения инерции в каждом сете я предлагаю корректировать долю очков, которые могут быть выиграны на подаче, после каждого гейма. В расчете коэффициентов корректировки я использую как счет сета (с учетом количества выигрышей на подаче соперника), так и доли очков, выигранных теннисистами на подаче.

Прогностическая сила этих двух переменных в некоторой степени совпадает. Как бы то ни было, в некоторых случаях одна из этих переменных позволяет получить ценные сведения, а другая не позволяет. Рассмотрим в качестве примера матч между игроками с равными шансами на победу и сравним счет 3:3 со счетом 4:2. Доли очков, выигранных соперниками на подаче, могут быть одинаковыми, однако игрок, ведущий со счетом 4:2, с большей вероятностью может победить во втором сете (а следовательно, и в третьем). Точно так же доли очков, выигранных соперниками на подаче, могут оказаться различными и при достижении счета 3:3, несмотря на его равенство.

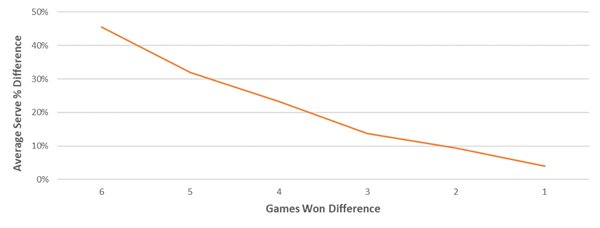
Для определения коэффициента корректировки доли очков, которые могут быть выиграны на подаче, и применения этого коэффициента после каждого гейма я использую значения вероятности победы в сете для каждого игрока, в основе которых находятся модели 30 000 матчей. На приведенном ниже графике эти значения показаны применительно к матчу между игроками с равными шансами на победу. Например, если в ходе шести геймов имел место один выигрыш на подаче соперника (со счетом 4:2), предполагаемая вероятность победы лидера в сете составляет 88 %. Согласно моей модели, в этот момент матча лидеру принадлежат 88 % надлежащей корректировки доли очков, которые могут быть выиграны на подаче.

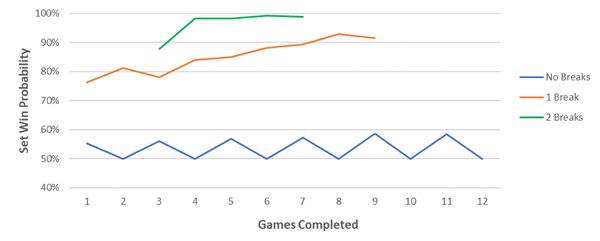
Помимо этого, после каждого гейма коэффициенты корректировок изменяются на основании наблюдаемой относительной силы подачи. Относительная сила подачи представляет собой разницу между долями очков, выигранных на подаче игроком 1 и игроком 2.

Чтобы выяснить зависимость между долями очков, выигранных на подаче, и счетами сетов (а вместе с ней и коэффициент необходимой корректировки), я смоделировал 30 000 матчей и вычислил разницу в долях очков, выигранных на подаче, связанную с различными счетами сетов. Например, средняя величина разницы между долями очков, выигранных на подаче, для завершенных сетов с разницей в два гейма (6:4 или 7:5) составляет +9 % в пользу победителя.

Благодаря использованию приведенных выше расчетов для динамичного определения коэффициентов корректировок долей очков, которые могут быть выиграны на подаче, после каждого гейма на протяжении матча можно построить нашу модель и сравнить результаты ее применения с реальными исходами матчей ATP. На приведенном ниже графике представлены 30 000 смоделированных матчей в сравнении со всеми матчами ATP начиная с 2010 г., для победителей которых предполагаемая вероятность выигрыша составляла 40–60 %.

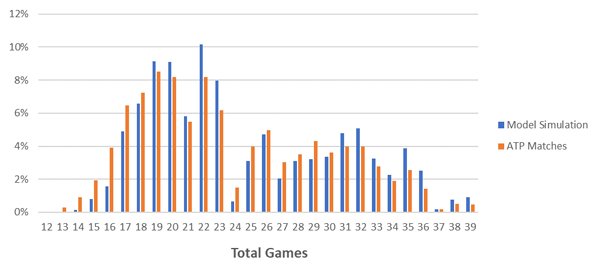
По всей видимости, эта модель обладает более высокой эффективностью по сравнению с исходной моделью, которая была описана в первой части статьи. Тем не менее она недооценивает тоталы геймов, составляющие не более 18. Это указывает на то, что модели не хватает динамичности применительно к матчам с большим преимуществом одной стороны.

Поскольку в основе системы оценки игры в теннисе находятся сеты, спортсмен, проигравший один или два гейма в ходе сета, может утратить интерес и (или) предпочесть сберечь силы и сохранить концентрацию внимания для следующего сета. Я подозреваю, что для отражения этого факта (а также для более общего отражения краткосрочной инерции) в модель необходимо включить фактор инерции в ходе сета, который дополнит описанные выше корректировки, осуществляемые в перерывах между сетами.

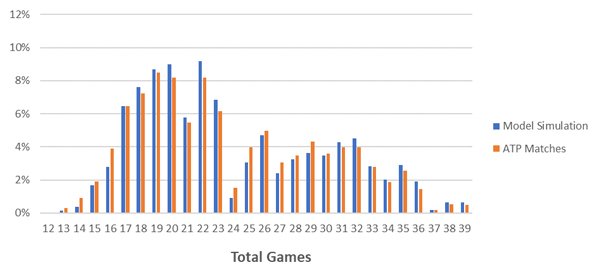
Не располагая данными о различных геймах, я вычислил величину этого фактора благодаря моделированию. В результате я выяснил, что модель должна очень быстро приспосабливаться к эффективности игры в ходе сета.

Коэффициент корректировки долей очков, которые могут быть выиграны на подаче, в ходе сета почти в два раза превышал тот же коэффициент в перерывах между сетами. Благодаря моделированию еще 30 000 матчей можно увидеть, что добавление фактора инерции в ходе сета повышает точность модели.

Доли очков, выигранных на подаче, и ставки на тотал матча

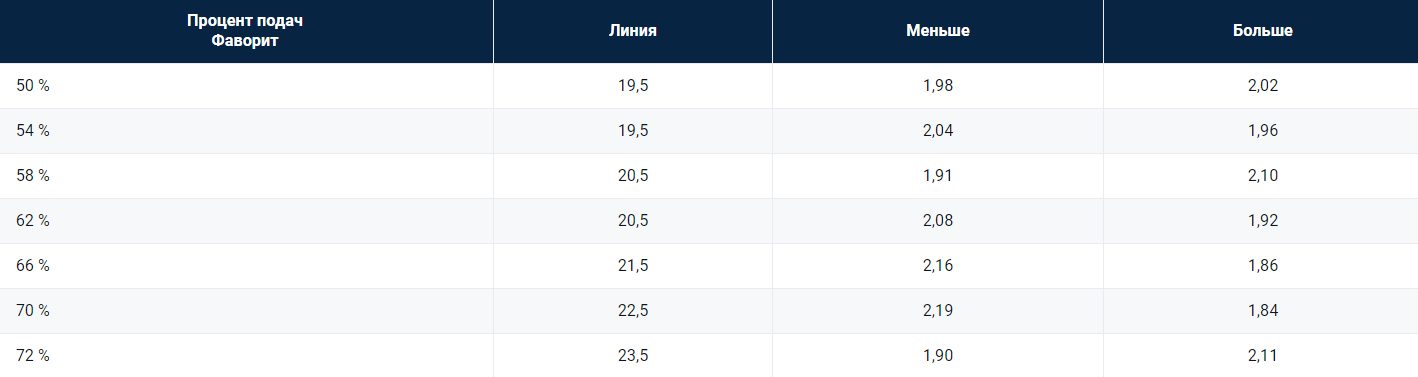
Теперь нашу модель можно использовать для оценки ставок на тотал матча. Прежде всего давайте посмотрим, как изменится рынок ставок на тотал геймов после изменения долей очков, которые могут быть выиграны на подаче в ходе матча между игроками с равными шансами на победу. В приведенной ниже таблице представлены результаты моделирования 10 000 матчей для каждой доли очков, которые могут быть выиграны на подаче, на рынке без маржи.

По мере увеличения доли очков, которые могут быть выиграны на подаче, с 50 % до 72 % уровень линии тотала геймов повышается с 19,5 до 25,5.

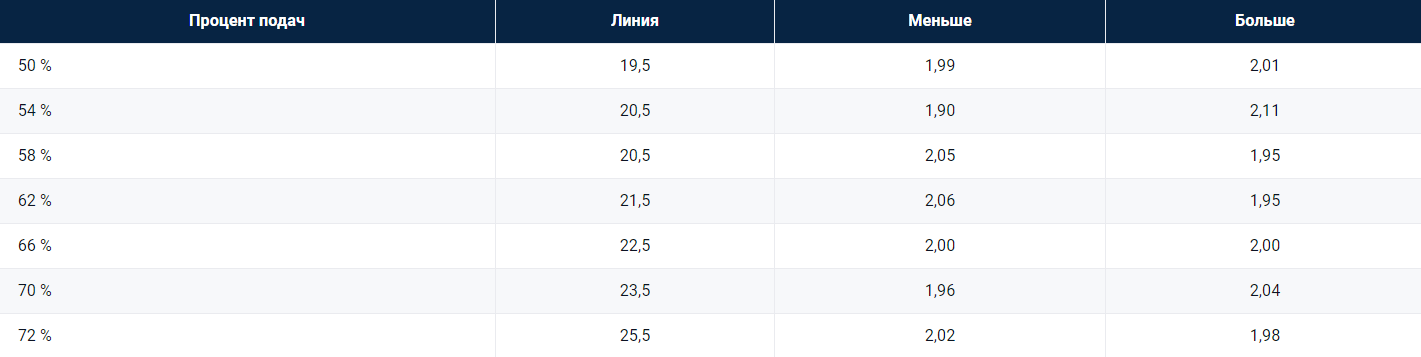
Если доля очков, которые могут быть выиграны на подаче, превышает 72 %, ставка на как минимум 26 геймов (два сета с тай-брейком) становится фаворитной. Например, в числе 50 лучших спортсменов ATP игроками с наибольшей долей очков, выигранных на подаче, являются Изнер и Федерер: они выигрывают на подаче около 72 % очков.

В ATP участвуют лишь несколько спортсменов, матч между которыми оправдал бы тотал 25,5. В таком матче должны сойтись два игрока с сильной подачей и слабым приемом, обладающие равными шансами на победу. Что произойдет с рынком, если в матче участвуют игроки с неравными шансами на победу, включая фаворита, ставки на выигрыш которого принимаются с коэффициентом 1,50?

Доли очков, выигранных на подаче, и ставки с гандикапом

Рассмотрим вопрос гандикапов матчей. Изменяя значения доли очков, которые могут быть выиграны на подаче фаворитом или аутсайдером, приближенно к 64 % – средней величине доли очков, выигранных на подаче в ATP, можно изучить зависимость коэффициентов ставок на матч от линии гандикапов для различных геймов.

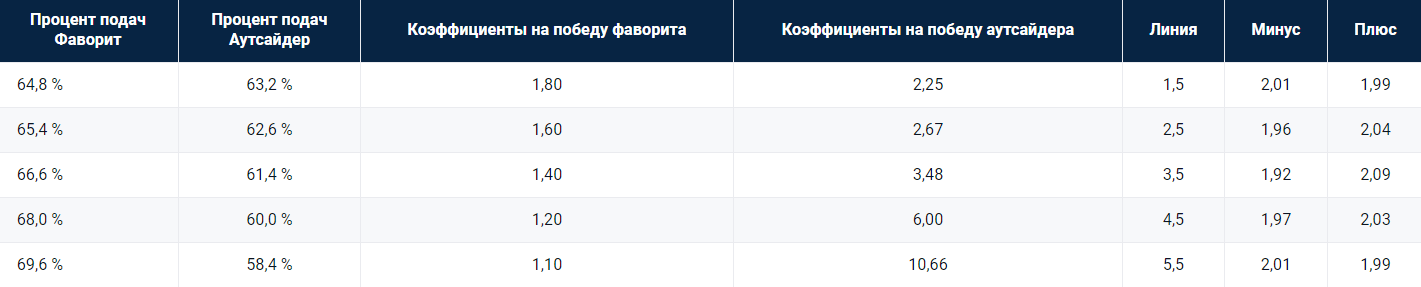
Сверка этих данных со сведениями о рынках ставок на теннис Pinnacle показывает, что модель хорошо откалибрована. В качестве заключительного шага к оценке каждого отдельного матча необходимо спрогнозировать доли очков, которые могут быть выиграны на подаче каждым игроком, и учесть эффекты предвзятости, связанные с конкретными игроками. При этом, возможно, понадобится корректировать факторы инерции: это поможет отразить закономерности в игре определенных игроков. О ряде этих закономерностей я рассказывал в другой моей статье.

В результате добавления двух динамичных переменных инерции моя модель тенниса ATP становится хорошо откалиброванной моделью, которую можно использовать для оценки рынков ставок на геймы, сеты, матчи и тоталы и ставок с гандикапом на основании долей очков, которые могут быть выиграны на подаче.

В качестве дополнительного шага можно учесть эффекты предвзятости, связанные со счетом или определенными теннисистами. Например, снижается ли вероятность того, что спортсмен выиграет гейм на своей подаче в ситуации, когда ему грозит опасность отдать сет, если, скажем, счет составляет *4:5 или *5:6? Модель, в которой учитываются такие эффекты, легко можно применять во время игры.